Saludos, Alexcore.
Realmente no sé si todavía tienes interés en la pregunta que has subido al post, y tampoco tengo idea sobre qué tipo de fuelles quieres animar, ya que no has subido imágenes. Pero me ha gustado tu pregunta y, como decimos aquí en Cuba, he quedado “enganchado” con ella y ciertamente me la he tomado como un reto. Resulta que te quiero proponer la animación de un fuelle, aunque te advierto que no soy bueno para nada animando. Pero en esencia la animación, como te respondí en tu post, tiene que venir luego que logres los efectos de la deformación del fuelle propiamente dicho. Bueno, y el clásico fuelle que se me ocurrió animar es un…. Acordeón.
Vamos a hacer un acordeón, cuyo fuelle se deforme, y al final te pongo la animación, aunque estoy seguro que habrá algún solidworker que logre una mejor animación pues, te repito, no soy bueno en eso.
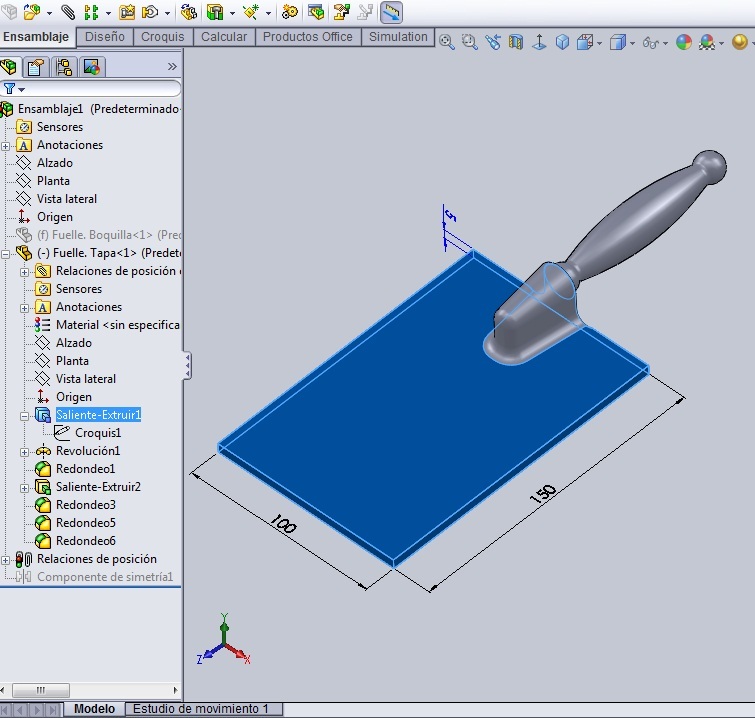
El acordeón que te propongo, en aras de que se entienda el procedimiento es lo más primitivo que se haya visto, pues no vale desgastarse en detalles tales como botones, correas, redondeos y otras cosas, que luego pueden ser incorporados. Así que lo primero que diseñamos es una caja normal y corriente de 100 x 150 x 50 mm, e inmediatamente abrimos un archivo de ensamble.
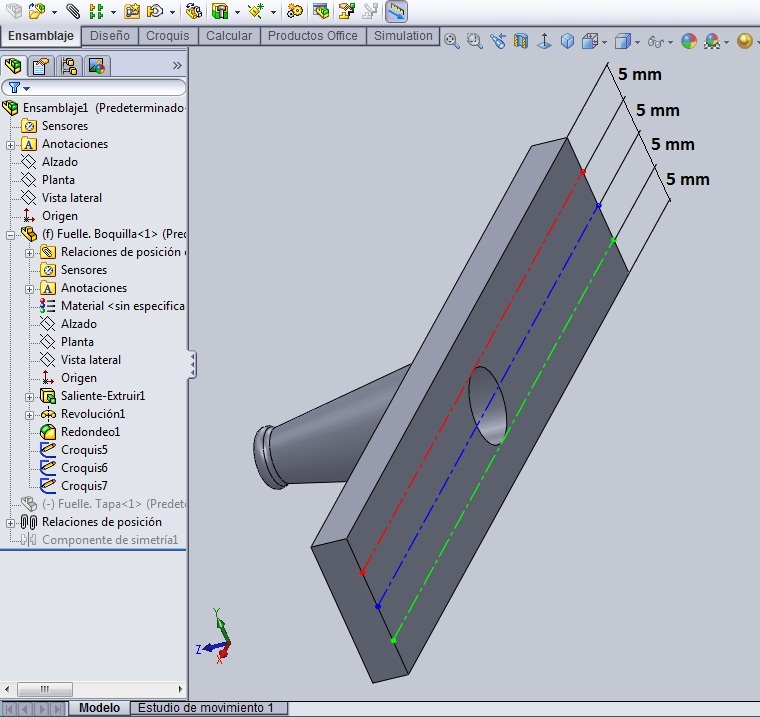
En ese mismo ensamble incorporamos otra caja a la izquierda de la fija, y les alineamos las caras frontal y superior como se muestra en el Dibujo 1, de manera que la segunda tapa se pueda mover con relación a la primera solo a lo largo del eje ‘z’. Nombramos el ensamblaje: ‘Acordeón’.
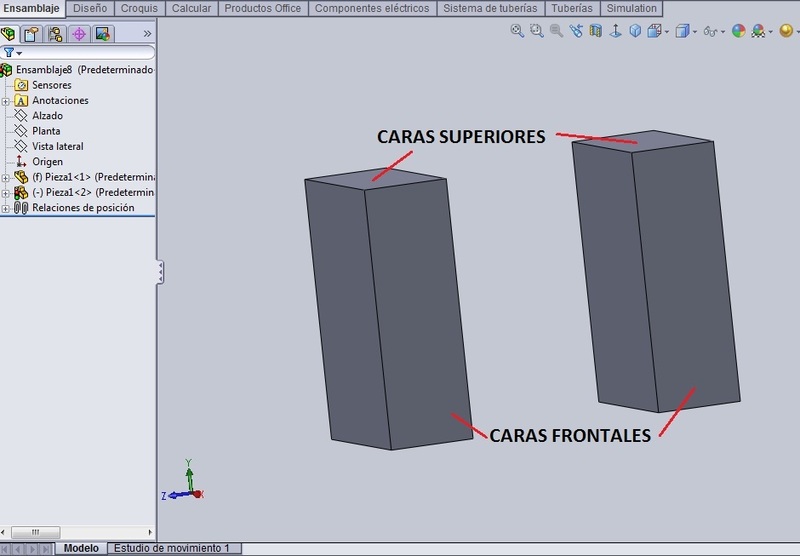
Lo primero que vamos a hacer, para facilitar las operaciones, aunque parezca innecesario, es separar las caras de las tapas que están enfrente la una de la otra a una distancia de 200 mm, y luego de esto, abrimos el árbol de operaciones donde están las relaciones de posición, y borramos esta relación. No existe la relación luego de borrarla, pero sabemos que las cajas están separadas a 200 mm.
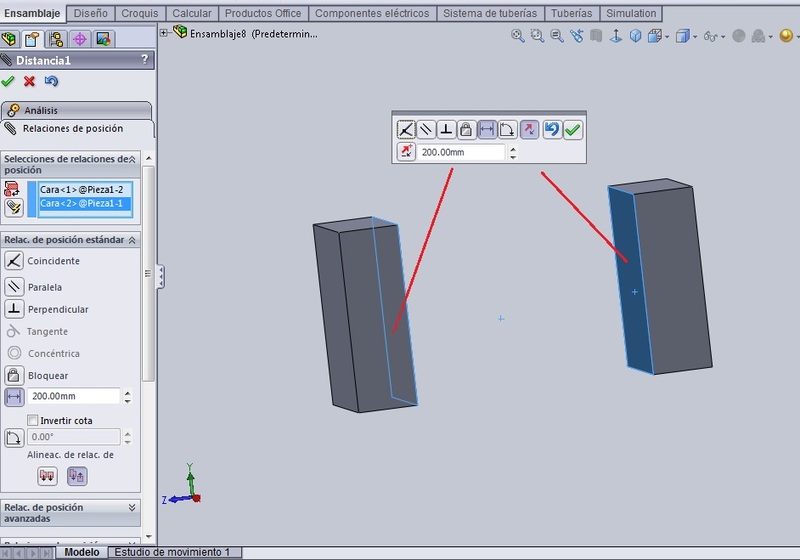
La animación del fuelle, como la de los muelles, depende de qué tanto se separan o acercan las piezas con quienes ellos topan por los extremos, por eso es conveniente elaborar el fuelle en el contexto del ensamblaje. Por otro lado, vamos a emplear una matriz, y uno de los elementos sintácticos de la operación ‘Matriz Lineal’ es la distancia con la que se van a multiplicar los componentes de la misma. Pero, si vamos a encoger y estirar el fuelle, manteniendo constante la cantidad de elementos de la matriz, entonces lo que va a variar en la misma es la distancia entre ellos. Por eso convenientemente hacemos lo siguiente.
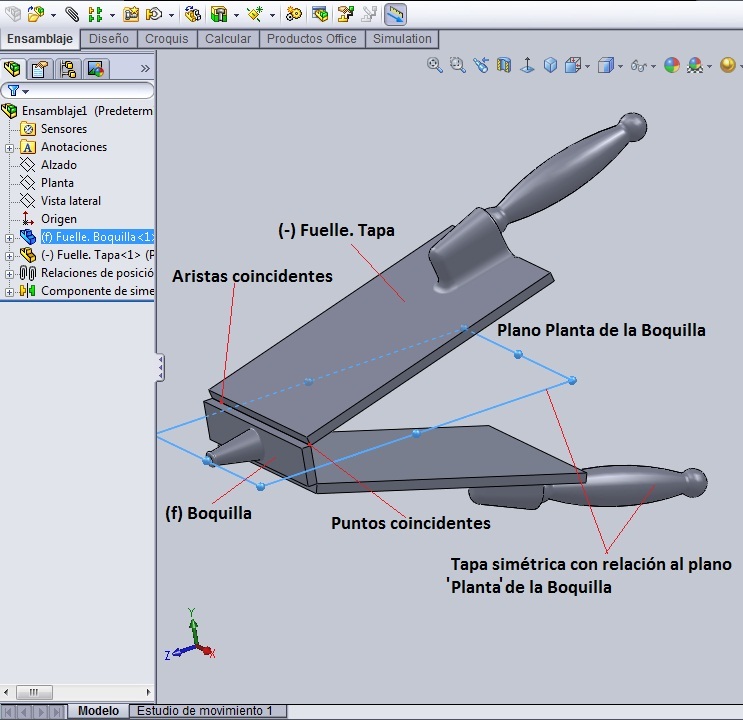
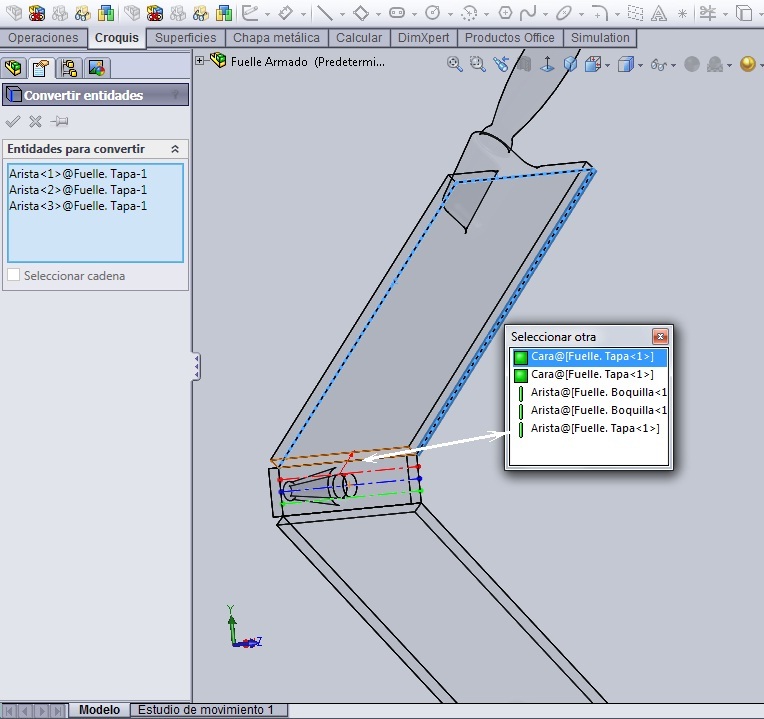
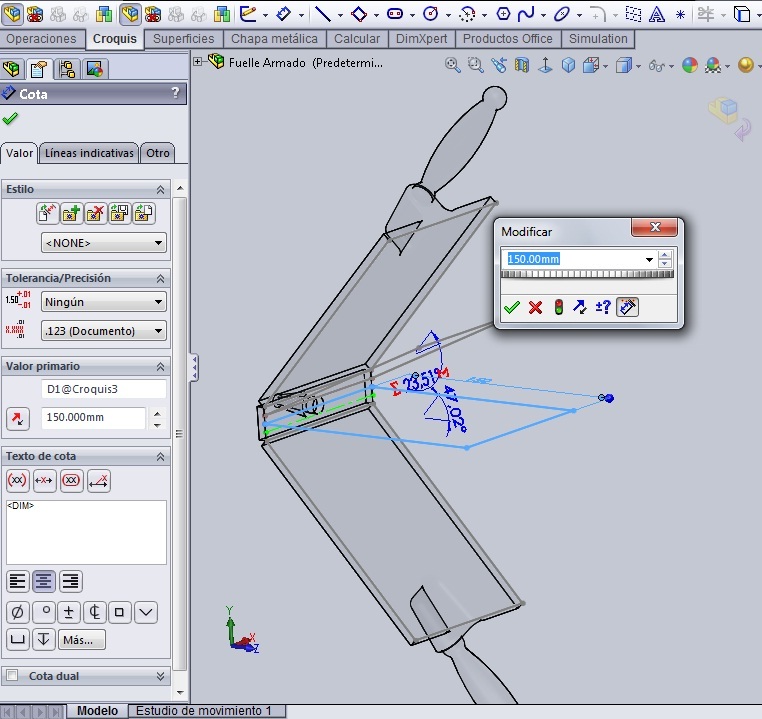
En el mismo ensamblaje abrimos un croquis en el plano transversal a las caras, que en mi caso es el Plano Lateral y, cuando aparezca la inferencia desde el origen del croquis, trazamos una recta horizontal relativamente pequeña que todavía no conectamos a ninguna parte. La recta, toda vez que se trazó sobre la inferencia que comienza en el origen del croquis, se va a ver en negro, pero los puntos extremos, como no están completamente definidos, se van a ver en azul.
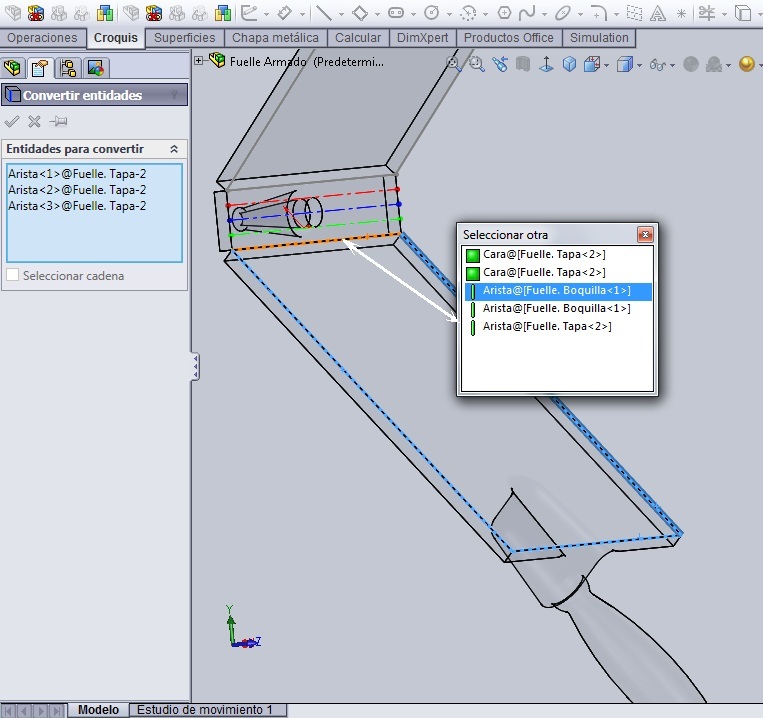
Las únicas relaciones de posición son: hacer coincidir los puntos extremos de la recta con las aristas de ambas cajas que se señalan en el dibujo. Haciendo coincidentes los extremos de la recta con las respectivas aristas de las tapas el croquis de la recta se define completamente, pero…… en contexto. Es decir, sin dimensiones concretas.
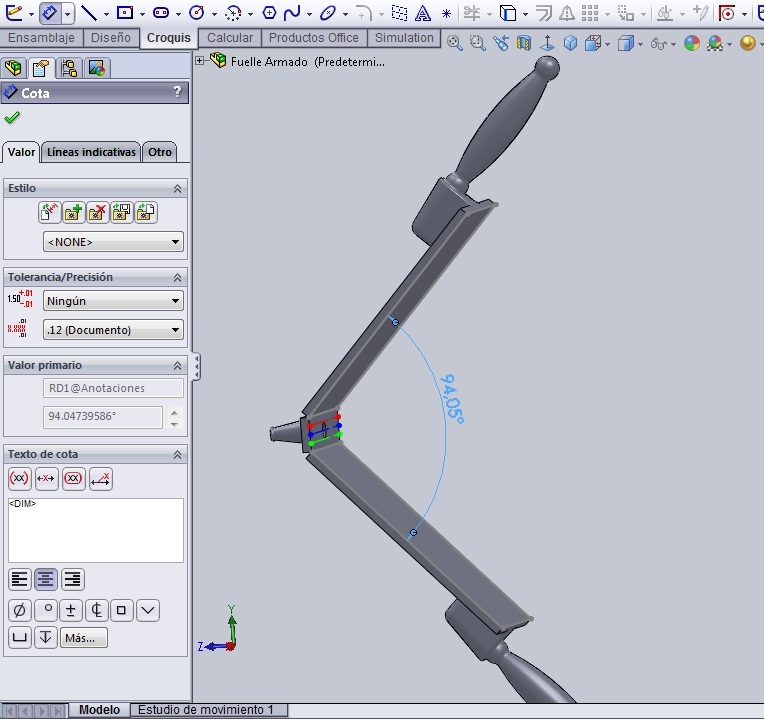
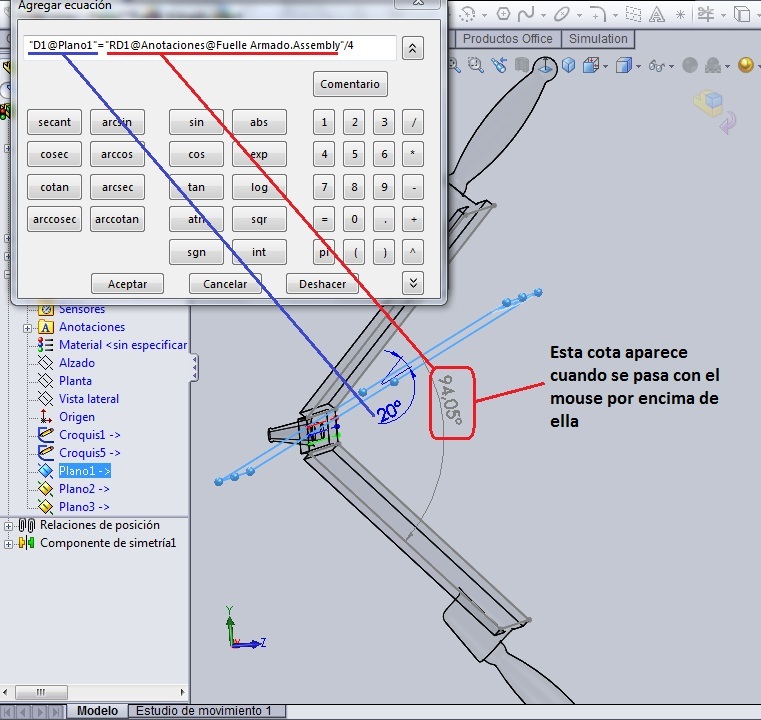
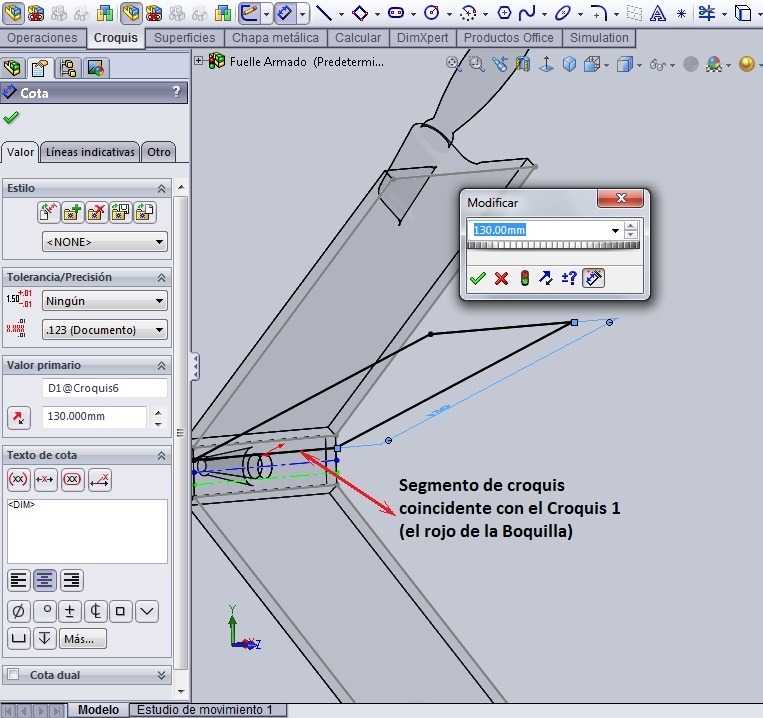
Sin embargo, como nos va a hacer falta la dimensión de la separación entre los elementos de la futura matriz, tendremos que acotar la recta. Ya de antemano sabíamos que las cajas estaban a 200 mm la una de la otra, pero al estar el croquis completamente definido y tratar de poner una cota demás, va a salir el cartelito que se muestra en el dibujo.
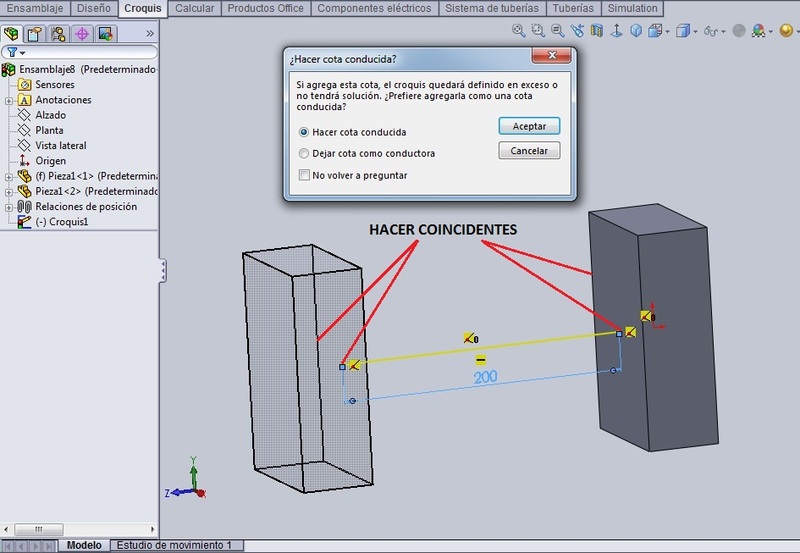
Aquí hay que aceptar que se quede la cota, pero como conducida. Ya se puede cerrar el croquis de la recta. Lo llamaremos: ‘Croquis 0’. Realmente lo puedes llamar como quieras y el predeterminado del programa será Croquis1, pero yo quiero emplear esa denominación de croquis para los elementos de la matriz.
Ahora (y esto lo hacemos siempre que tengamos dudas que las cosas están saliendo bien) movemos la caja que no está fija hacia un lado o hacia otro, y oprimimos el botón del semaforito ‘Reconstruir’. Si todo lo hemos hecho bien, entonces verás que luego de ‘Reconstruir’, para la nueva posición de la Caja 2 la recta del Croquis 0 adoptará también otra dimensión. Así que volvemos al estado anterior: separamos de nuevo las cajas a 200 mm la una de la otra en el ensamblaje y luego borramos nuevamente esa relación.
Para construir el fuelle en el contexto del ensamblaje ocultamos, o hacemos transparente la caja móvil para que no interfiera. Yo la hice con transparencia.
Ahora, en el Menú ‘Ensamblaje’ se abre una nueva pieza y la misma se hace en la cara que se señala de la caja fija (f).
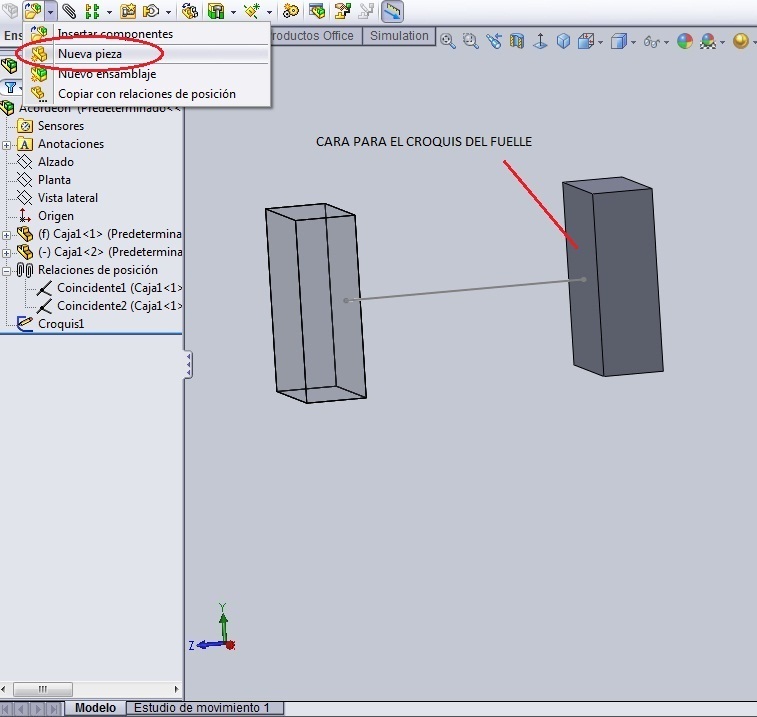
Cuando toques con el ratón esa cara, la pieza se pondrá semitransparente y en el árbol de operaciones aparecerá una nueva pieza con las operaciones en azul. Haces girar convenientemente el ensamblaje y dibujas un rectángulo coincidente con las aristas de esa cara de la caja fija (saldrá un rectángulo de 100 x 150 mm). Este será el Croquis1. Se cierra el croquis.
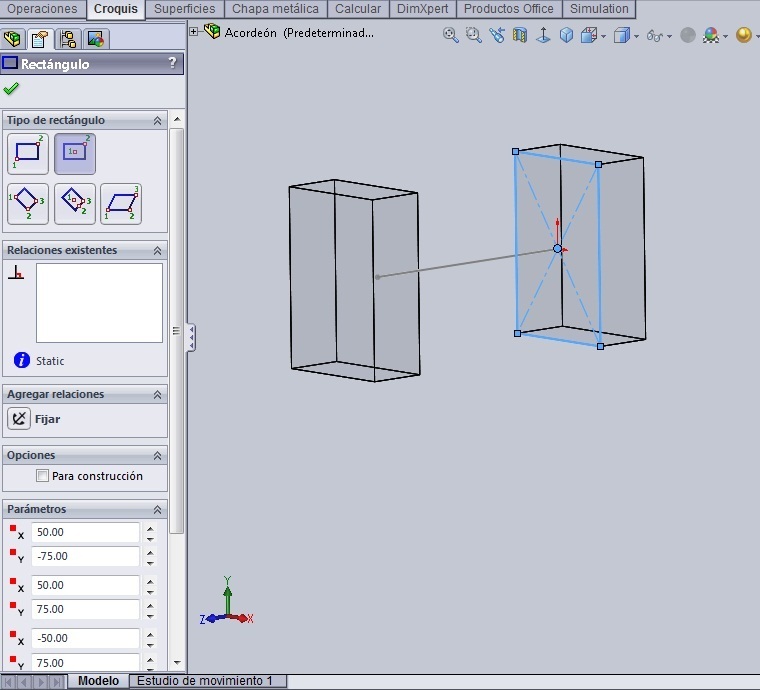
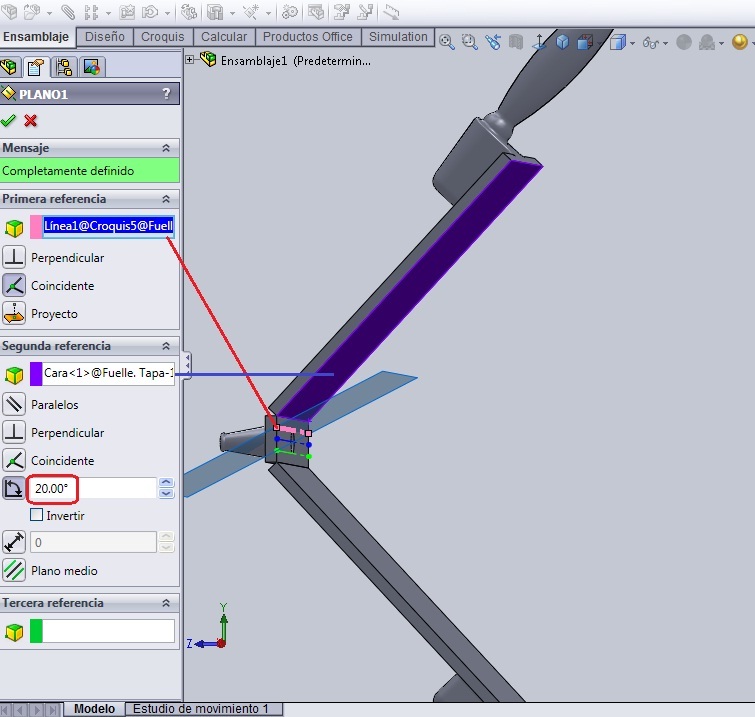
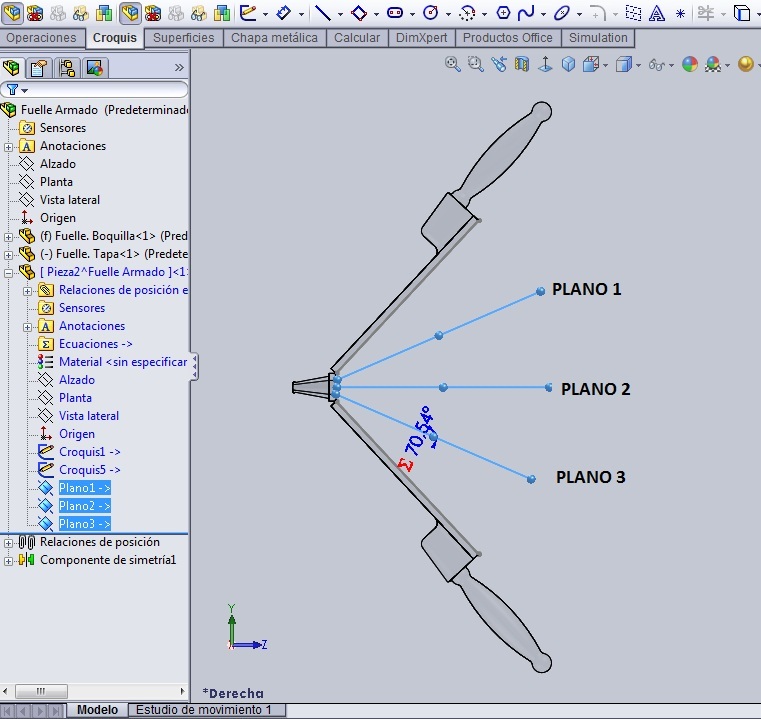
Seguimos en el modo ‘Nueva Pieza’. Tomando como referencia la cara donde se ha hecho el Croquis1, creamos el Plano 1, paralelo a esa cara, que se separe de la misma 10 mm. En él construimos un nuevo rectángulo de centro, que sea 10 mm inferior al anterior por cada lado, es decir 80 x 130 mm. Este será el Coquis2. Se cierra el croquis.
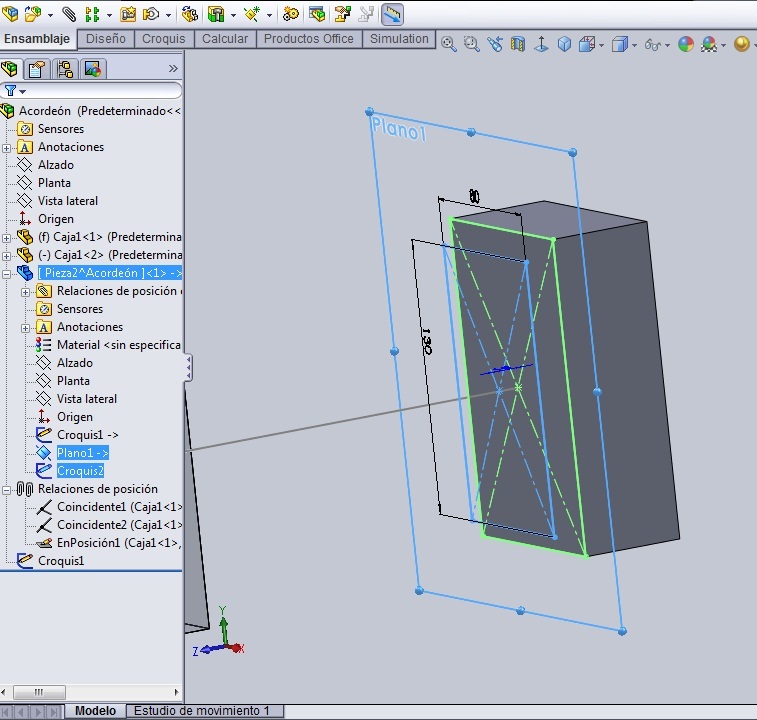
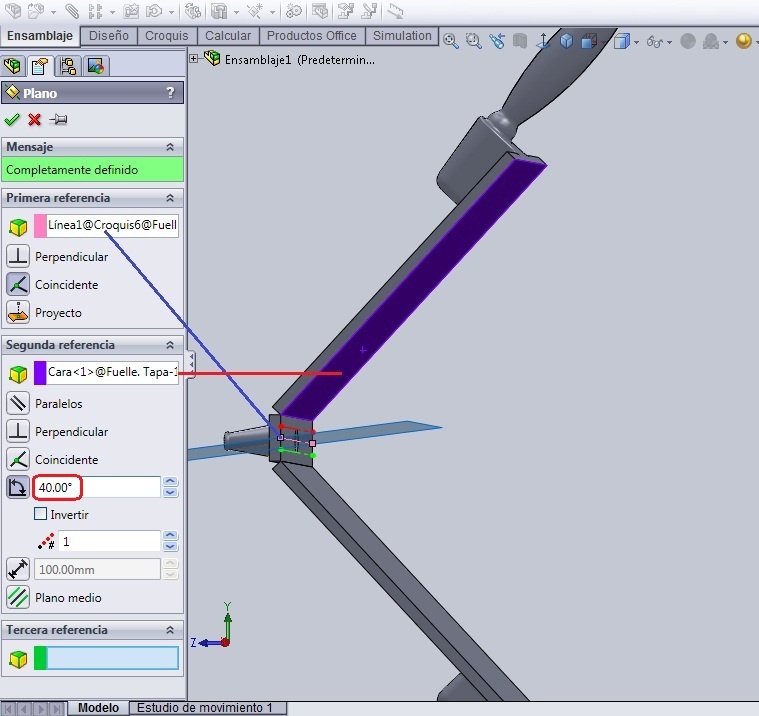
Por último, creamos el Plano 2, paralelo al plano 1, que se separe del mismo 10 mm, y sobre él dibujamos, con un rectángulo de centro el Croquis3, igual al Croquis1. Cerramos el croquis.
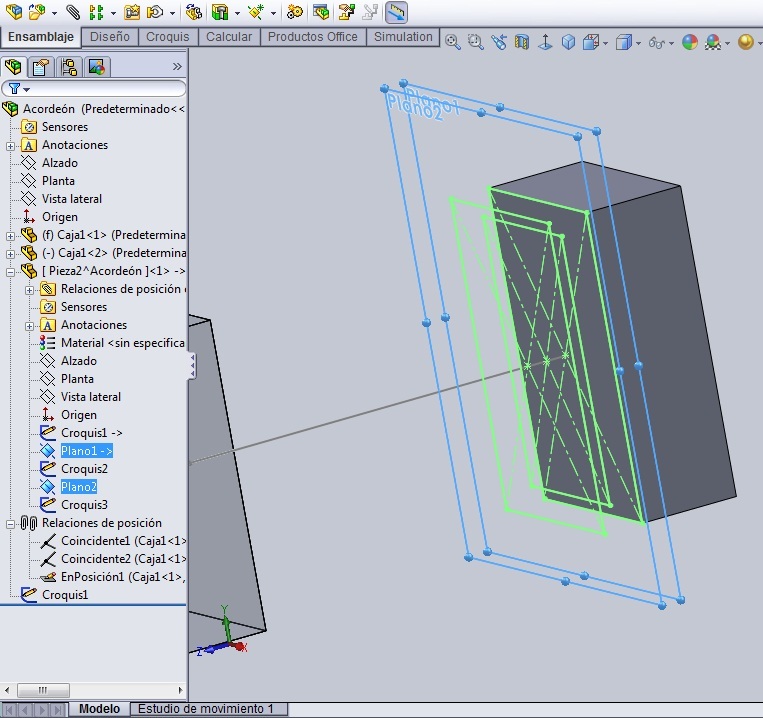
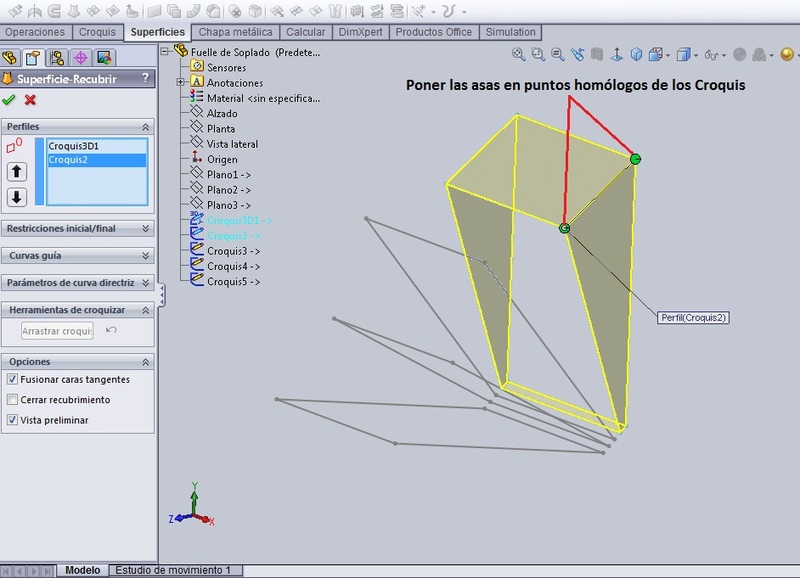
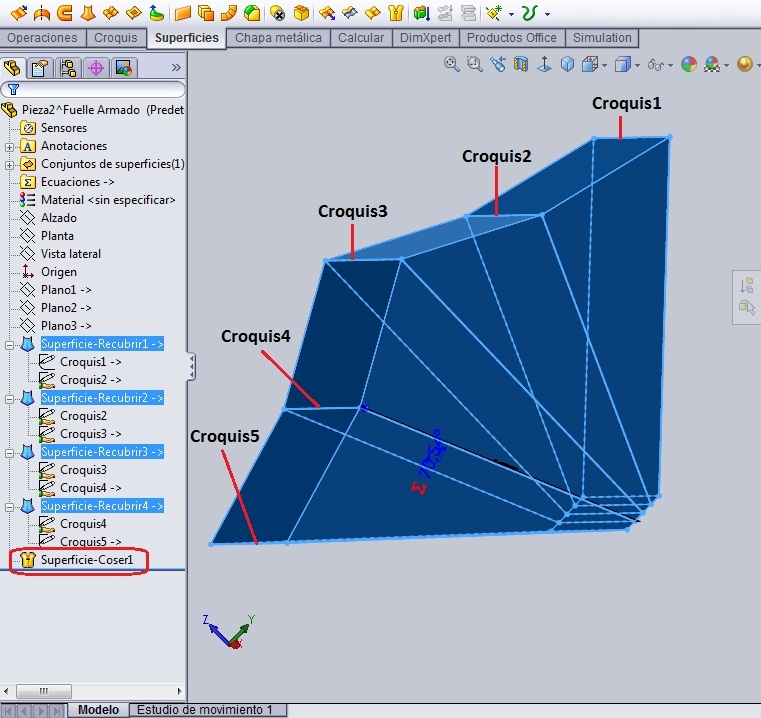
Ya existen todos los croquis necesarios para crear el ‘fuelle unitario’ compuesto de una superficie que nace en el Croquis1, desciende hasta el Croquis2, y luego vuelve a ascender hacia el Croquis3. Por eso en el menú ‘Superficies’ escogemos el comando ‘Recubrir Superficies’, y hacemos dos recubrimientos: Uno desde el Croquis1 hasta el Croquis2, y otro desde el Croquis2 (que ya está en contexto de la operación anterior) hasta el Croquis3. Después de lo cual cosemos ambas superficies.
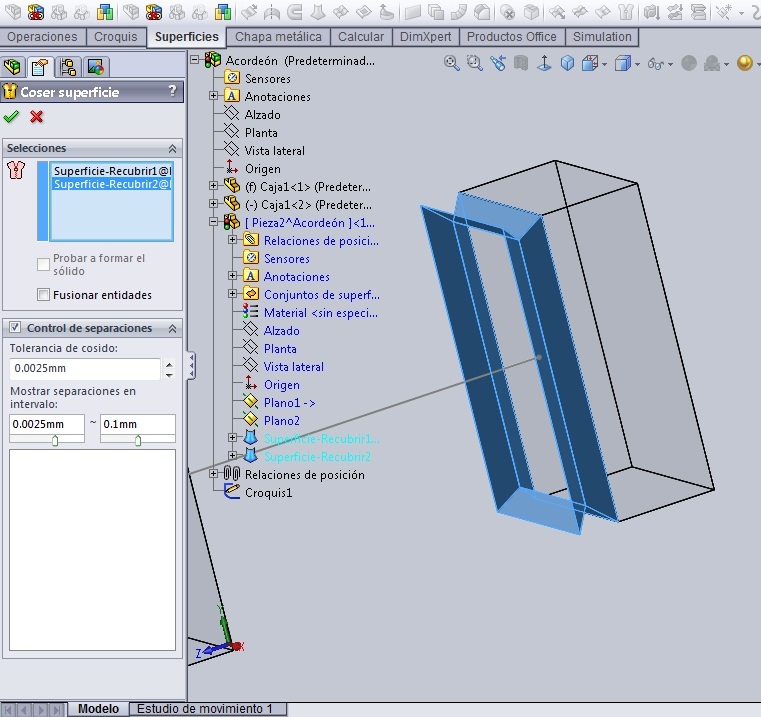
Empezamos a vincular parámetros. ¿Qué es lo que tenemos hasta ahora? :
1.- La distancia entre las cajas es de 200 mm;
2.- La distancia del Plano 1 a la cara que lo origina en la Caja fija es de 10 mm; por lo tanto esta distancia es igual a la distancia entre las cajas (200) entre 20;
3.- La distancia del Plano 2 al Plano 1 es la misma: 10 mm.
Ahora eso mismo lo planteamos con fórmulas en el ensamblaje. Pero como el Croquis0 fue creado en el marco del ensamblaje y no de la pieza que se está creando, entonces hay que cerrar el modo de ‘Nueva Pieza’ y, en Herramientas – Ecuaciones – Agregar, abrimos la barra para la primera ecuación.
Para crear la fórmula que expresa lo que se plantea en el punto 2 es necesario:
Hacer doble url encima de ‘Plano 1’ en el árbol de operaciones. Aparecerá en azul la cota que define la posición de ese plano. Si no la ves bien puedes hacer girar el ensamblaje. Cuando tocas la cota del Plano 1 con el ratón, el nombre de la cota aparecerá en la barra de edición de la nueva fórmula. Seguido de esto se pone el signo igual ‘=’ y se hace doble url en ‘Croquis0’ en el árbol de operaciones. Aparecerá la cota conducida de la recta de ese croquis, que tiene un valor de 200 mm. Igualmente se urlea sobre ella y la misma aparecerá en la barra de edición de la fórmula. Después de eso introducimos el signo de dividir ‘/’ y escribimos ‘20’. Quedará como se ve en el dibujo.
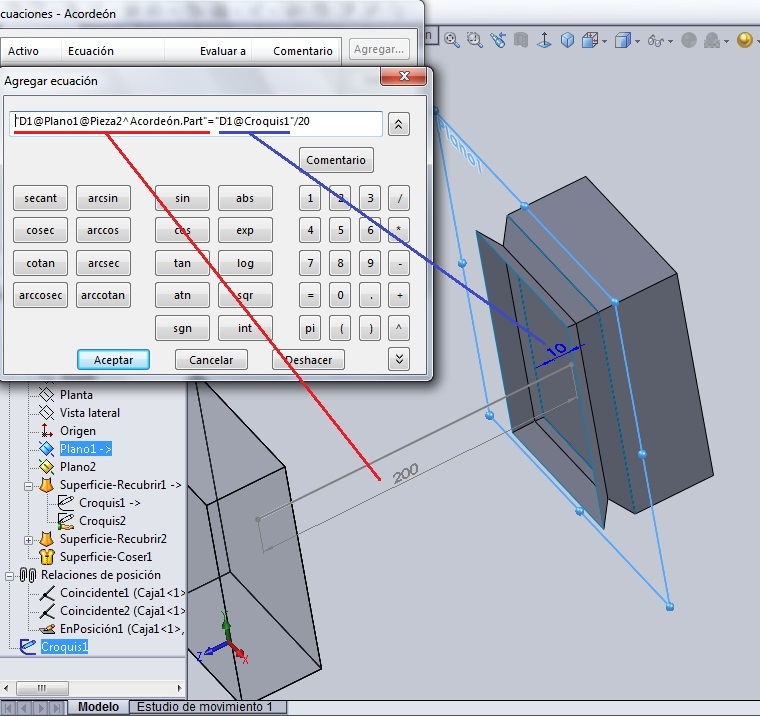
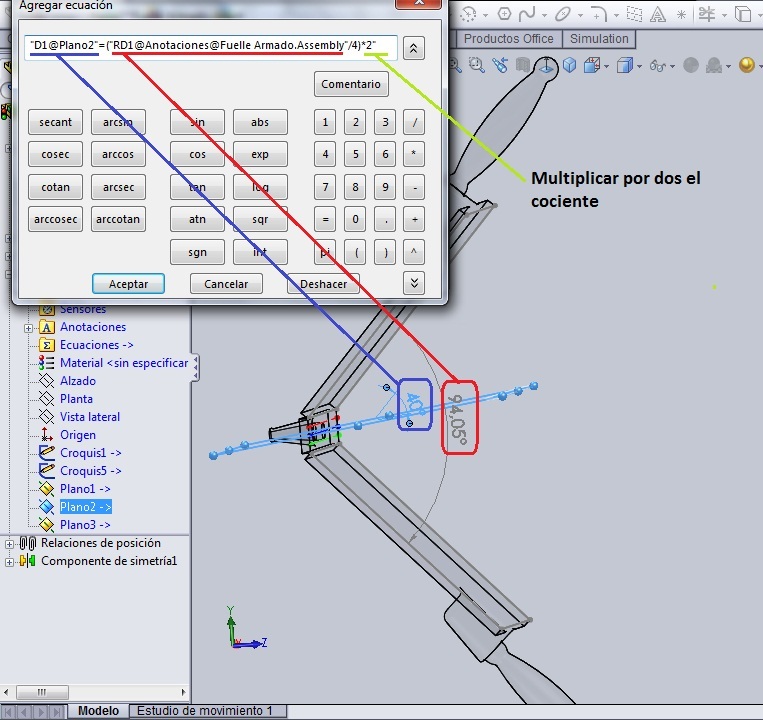
Para crear la fórmula que expresa lo que se plantea en el punto 3 es necesario:
Abrir la barra para la segunda ecuación en Herramientas – Ecuaciones – Agregar. Se verá que en el cuadro de ‘Ecuaciones’ ya existe la primera ecuación.
Se hace doble url en Plano 2 en el árbol de operaciones. Aparecerá en azul la cota que define la posición de ese plano. Se toca con el ratón dicha cota y la misma aparecerá en la barra de edición de la ecuación, seguido de lo cual se pone el signo igual ‘=’ y se hace doble url en Plano 1 en el árbol de operaciones. Encima del Plano 1 aparecerá la cota que lo define en azul, pero con el símbolo de ecuación delante porque ya anteriormente fue involucrada en una ecuación. Se urlea encima de la cota y la segunda ecuación se verá en la barra de edición como lo muestra el dibujo.
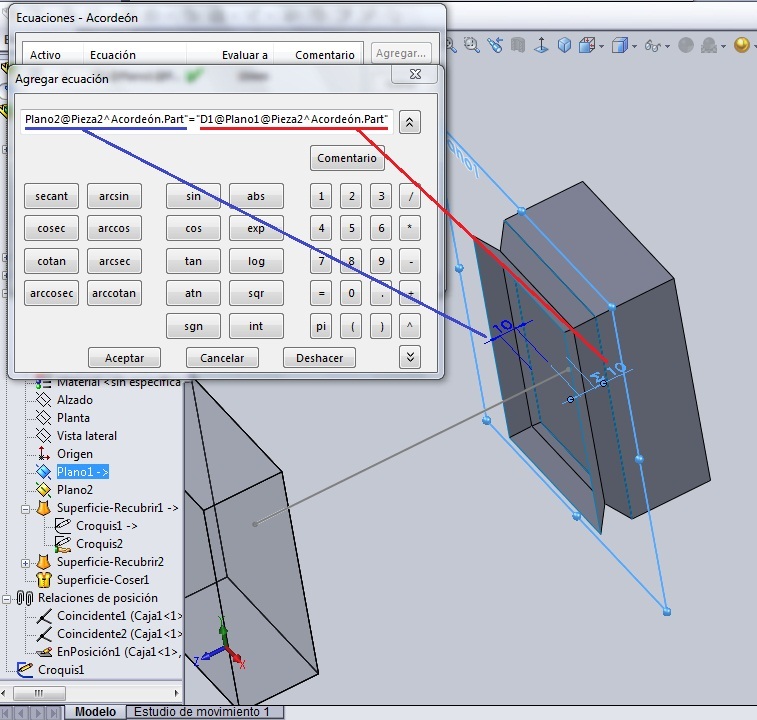
Nuevamente se comprueba lo que se ha hecho hasta ahora. El procedimiento es el mismo: se mueve la caja móvil hacia adentro o hacia afuera y, al ‘Reconstruir’ la primera vez, verás que la recta del Croquis0 se reconstruye, y al reconstruir por segunda vez, el ‘fuelle unitario’ se estirará o encogerá en correspondencia con el desplazamiento que se le dio a la caja móvil.
Nuevamente se separan las cajas a 200 mm. Seguidamente se borra la relación en el árbol de relaciones de posición y se reconstruye dos veces la pieza para que tanto la recta como el fuelle unitario tornen a la posición correcta.
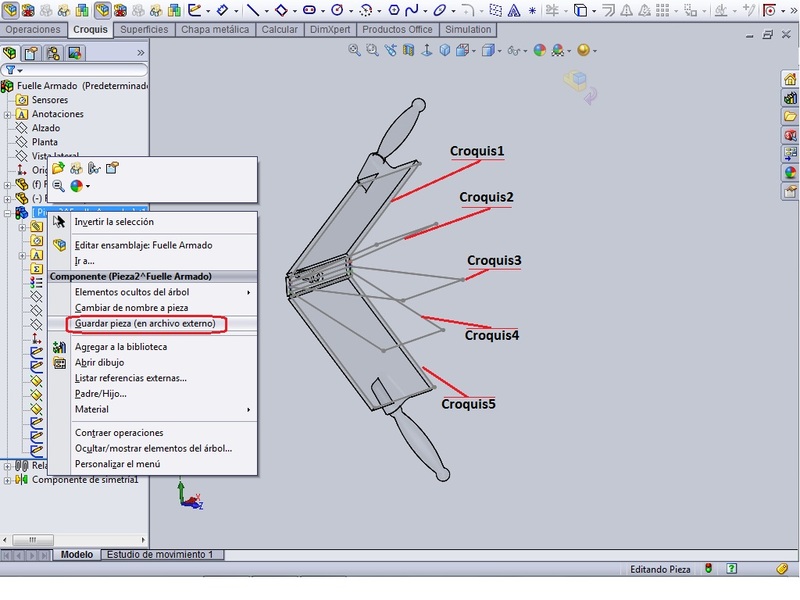
Guardamos la pieza que se está construyendo, dándole un url derecho encima, guardando la pieza dentro del ensamblaje, seleccionando que la dirección sea la misma que en el ensamblaje y se le denomina ‘Fuelle’.
Ahora solo queda hacer la matriz. Para ello nos colocamos encima del ‘Fuelle’ en el árbol de operaciones y dando url derecho seleccionamos ‘Editar Pieza’.
En el menú ‘Operaciones’ seleccionamos el comando ‘Matriz Lineal’. Para la dirección de la matriz se escoge la recta del Croquis0; la distancia entre elementos de la matriz es 20 mm y tomamos 10 fuelles unitarios (Superficie coser). La imagen se muestra como en la Figura.
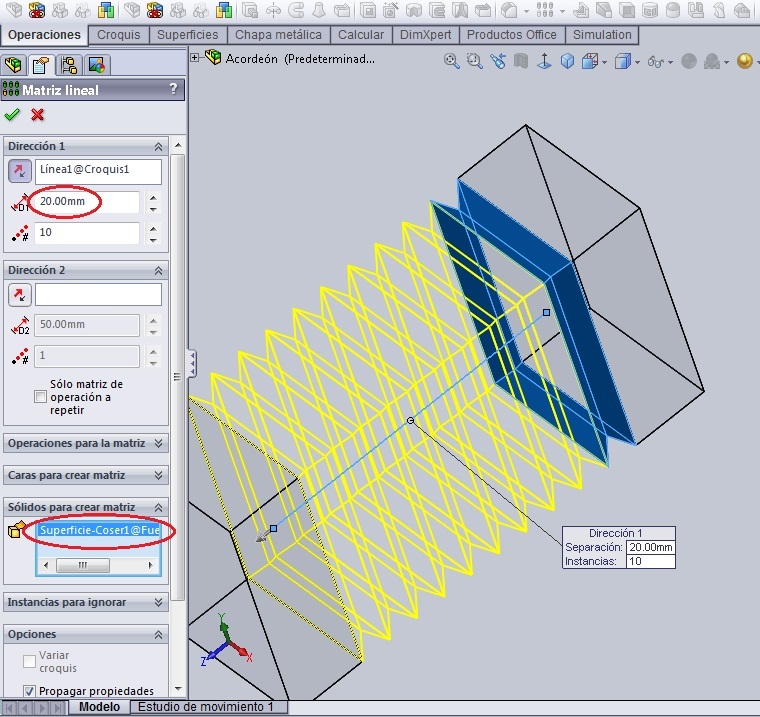
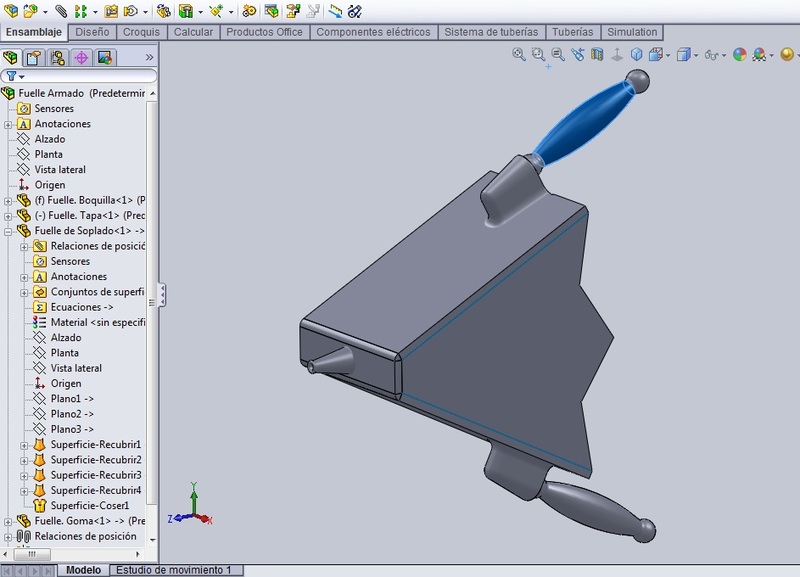
Al hacer url en aceptar, ya aparece el fuelle completo del acordeón. Salimos del modo ‘Editar Pieza’, quitamos la transparencia de la caja móvil y ocultamos el croquis de la recta que queda visible.
Pareciera que todo terminó, pero nos queda un punto. Y es que, como el acordeón lo mismo se estira que se encoge, la distancia entre los fuelles unitarios no siempre es 20 mm, como seleccionamos en la matriz. Esa distancia será igual a la suma de las distancias de los Planos 1 y 2 (que da 20 mm) o a la distancia del Plano 1 (que es 10) multiplicado por 2.
Para darle una expresión matemática a este planteamiento volvemos a: Herramientas – Ecuaciones – Agregar y abrimos una nueva ecuación. Hacemos doble url encima de la Matriz1 en el árbol de operaciones, y en el área de trabajo aparecerán los parámetros de la matriz en azul (distancia: 20 y cantidad de elementos: 10).
Se hace url encima del ‘20’ y el nombre del parámetro aparecerá en la barra de edición de la fórmula. Luego de esto se pone el signo igual ‘=’.
Se hace doble url encima del Plano 1 en el árbol de operaciones y aparecerá igualmente la distancia del Plano 1 (Σ10) en azul. Se hace url sobre el valor, y su nombre aparece en la barra de edición.
Por último ponemos en la barra el signo de multiplicar ‘*’ y el número ‘2’.
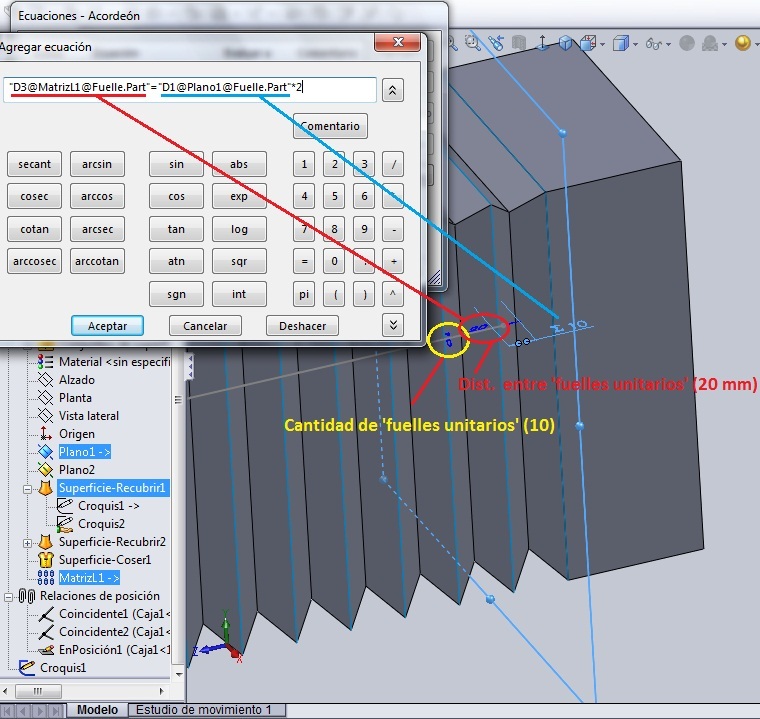
A veces el programa escribe los parámetros en planos diferentes y por eso no se ven muy bien, pero girando el ensamblaje los encuentras.
Ahora solo queda comprobar que lo que se ha hecho es correcto. Se acerca la caja móvil a la fija y se reconstruye dos veces. Se verá cómo el fuelle se encoge.
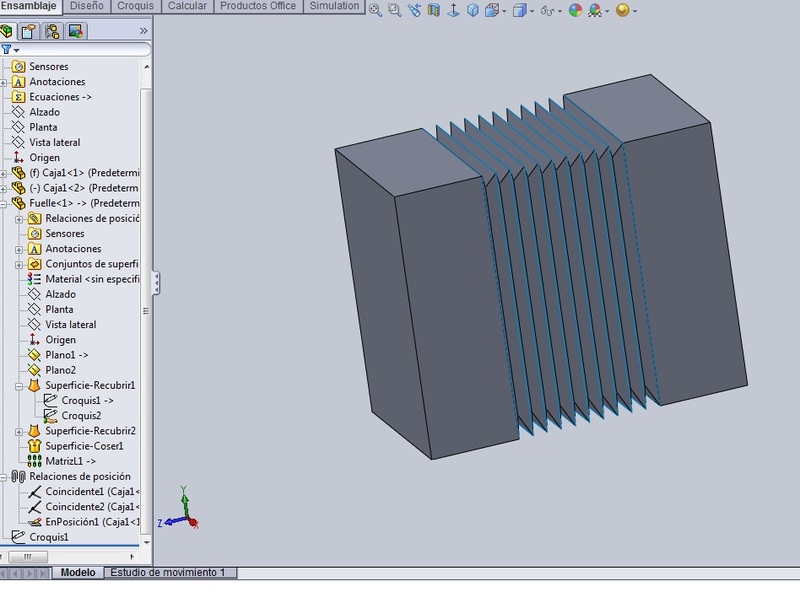
Y luego se separan las cajas y se reconstruye dos veces. Se verá cómo se estira el fuelle.
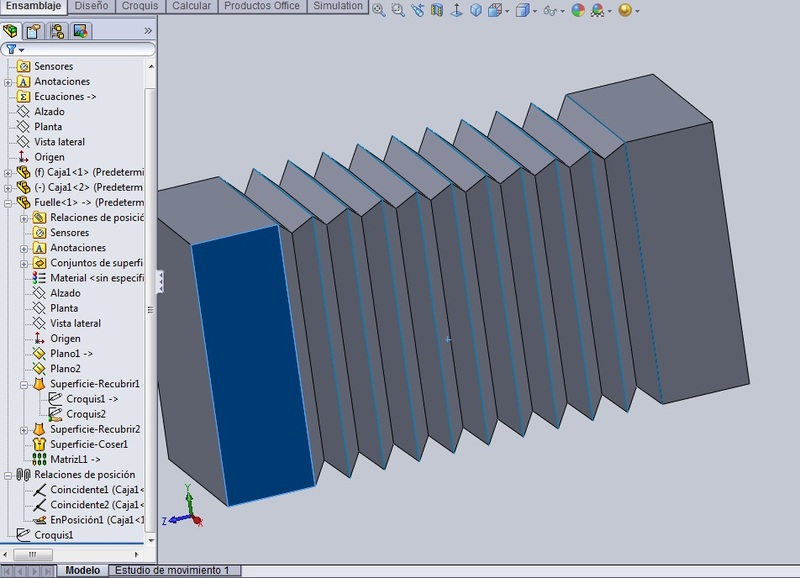
Lo último que nos queda es la animación. Te explico lo que hice:
Abrí un nuevo estudio de movimiento, seleccionando ‘Animación’ y corrí la línea del tiempo a 1 seg.
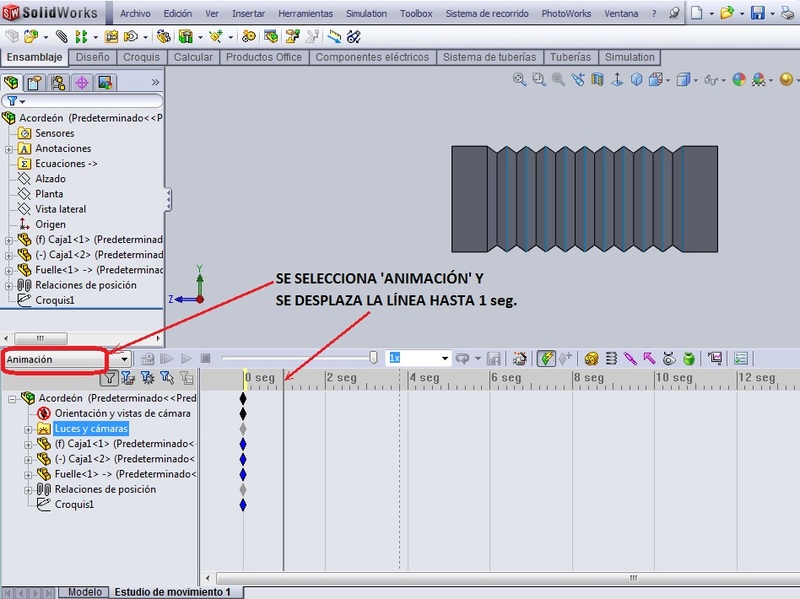
Recogí la caja móvil del acordeón a una distancia más o menos cercana de la caja fija y oprimí el botón ‘Calcular’. El fuelle del acordeón se animó.
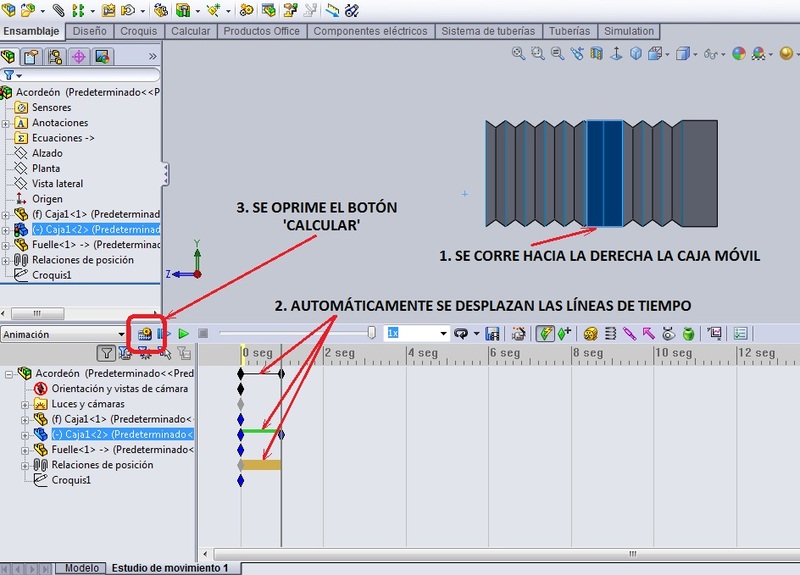
Ciertamente no escucho la musiquita, pero creo que se esmera en sacarla, jaja. Te anexo el archivo del Acordeón en SW2010. Bueno, esto me quedó bastante extenso, pero creo que se cumple el objetivo. Aquí tienes la animación del fuelle de un acordeón con movimiento lineal. Los detalles del acordeón y los renders se los dejamos a algún solidworker de este foro que ya los he visto verdaderos maestros en eso. Un saludo para ti y para todos nuestros foronautas.

![]()