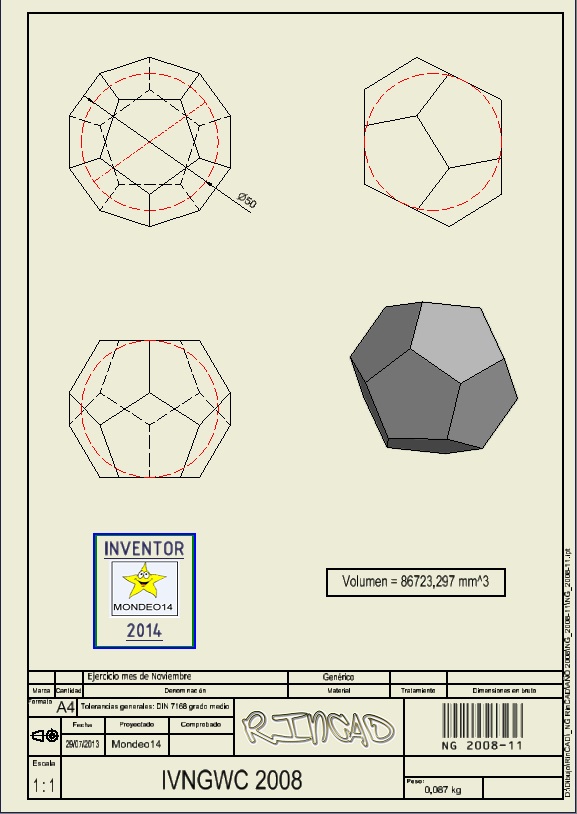
Hola, Corrijo pues mi imagen anterior.
Pues mi proyección de las aristas era errónea.
Salvo error; esto es lo que aprendí en la proyección diédrica de los compañeros anteriores
sin números de magnitud; hasta el momento.
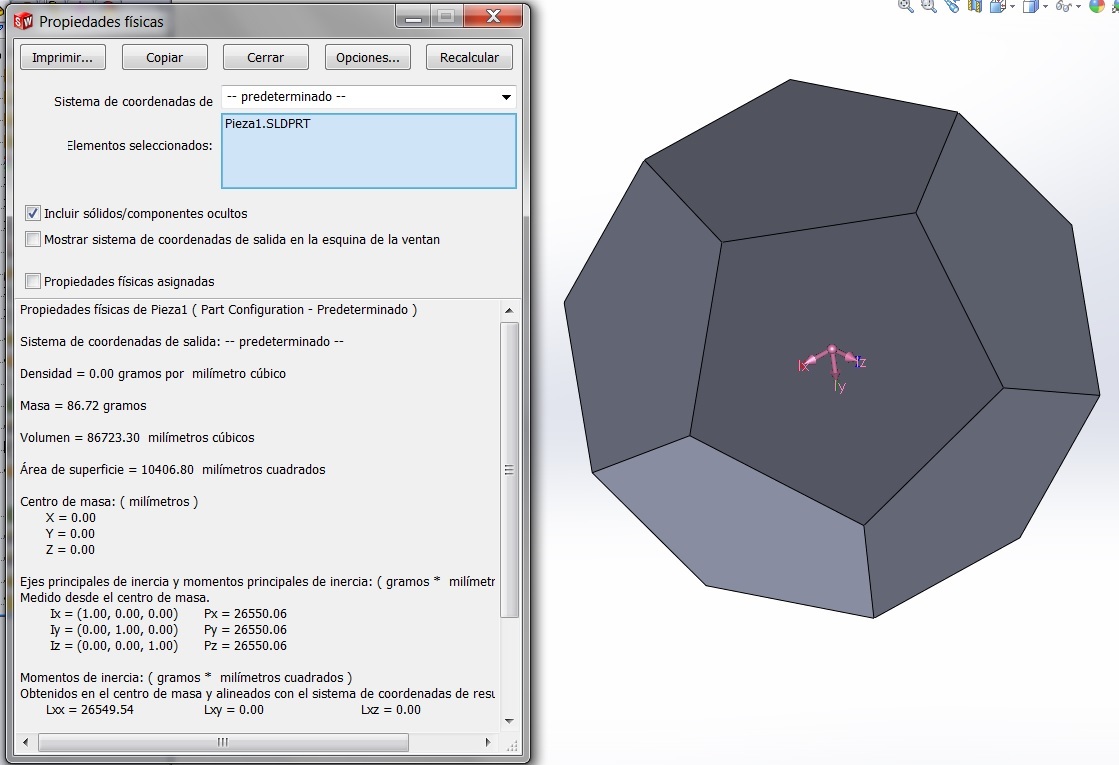
Imaginé solamente la idea de su esfera. Es tangente a sus doce caras. Y después revertí el abatimiento de su cara común; la cual es pentagonal.
Uno de sus vértices lo imagino en coordenada esférica y concéntrico desde un punto ajeno al poliedro y con centro en el punto (T).

Pertenece al mismo plano del diedro en el cual está apoyado una de sus doce caras y el radio de su coordenada esférica lo prevengo; como (h).
Así apoyado, una de sus verdaderas caras aledañas a la de apoyo en el diedro tiene dos vértices: llamados A y B.
Y como la proyección del dodecaedro en planta y alzado es un otro dato más y en si mismo: Se sabe que si por ellos por ellos pasaran sendos planos paralelos a la de apoyo, el perímetro de cada corte resultarían polígonos decagonales.
Así es verdad que se observa en proyección que: -cada lado de esos polígonos perimetrales que pasan por A o B, equivalen a su vez a la diagonal de cualquier pentágono-
En este ejercicio concretamente; uno de sus datos es que entre dos de sus caras iguales hay una magnitud imaginada como (h + h') .
El punto central, pues de todo el poliedro estaría centrado y ortogonal desde el centro de la cara de apoyo y entre esos dos planos paralelos que pasan por los vértices A y B. Se pueden pues; abatir en el diedro y después obtener las proporciones de h y h'. Con ellas llevarlas a alzado y restar.
En memoria de compañeros.

 -
-