Buenos días,
Dejo un ejercicio para el que quiera intentar hacerlo. Este ejercicio esta relacionado con este hilo AQUI. Los datos son los que hay el resto se ha de calcular.
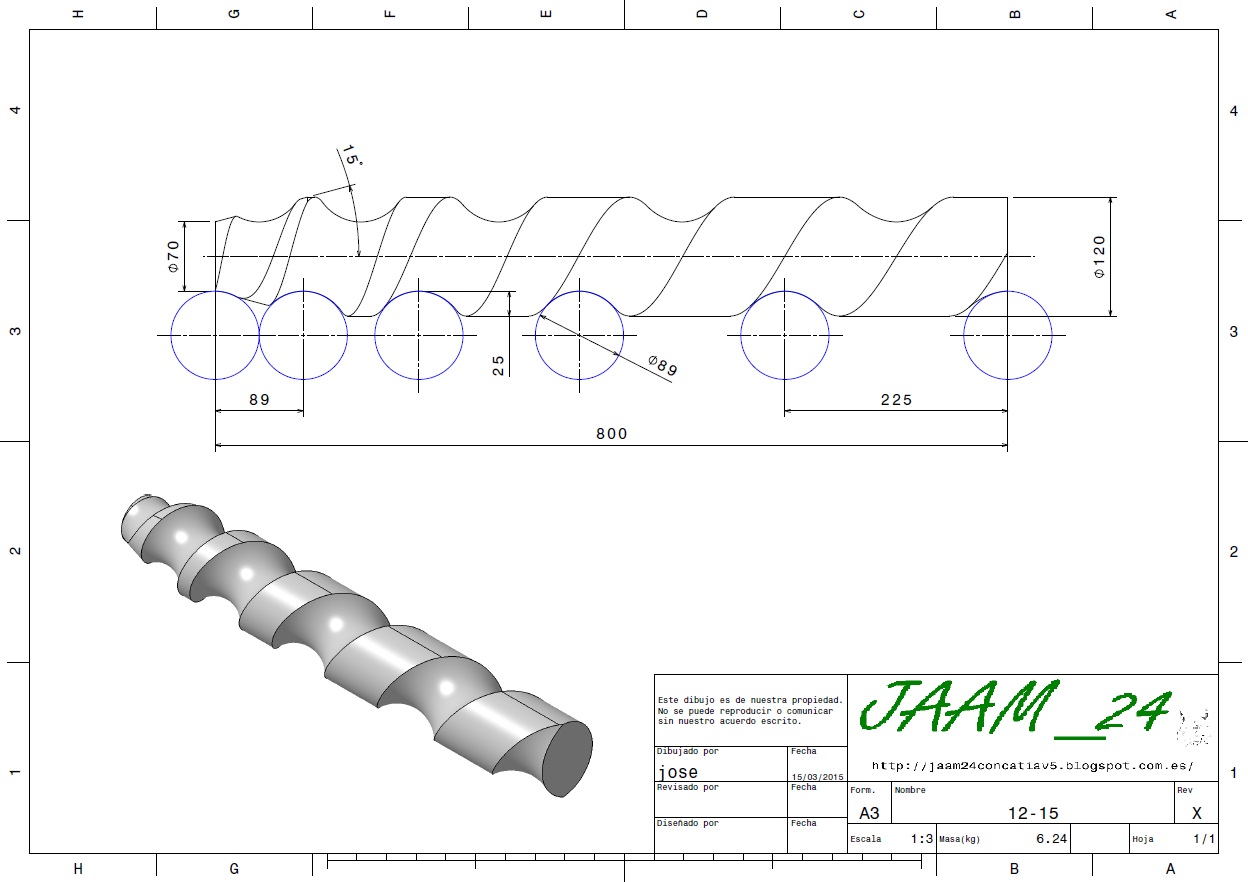

Saludos. ![]()


Me temo que mi solución no sea del todo académica. Como no se hacer una helix de paso variable hice una helix por cada tramo. Como no quedan tangenciales las he unido con Conect Curve.
En el extremo izquierdo he aportado un poco de creatividad pues el diámetro 70mm, con la inclinación de 15º no son compatibles con los 89 mm. Los he adaptado para que resten el material.
El archivo adjunto está en Catia R20 por si alguien lo desea estudiar. Un saludo.



Buenas
Luna, para hacerlo como has echo tu la hélice a de ser cónica y al radio del barrido añadirle una ley para que los radios aumenten con el paso.
Algo así
Saludos. ![]()

Siguiendo una antigua lección tuya en este foro he aprendido lo de la hélice de paso variable. Empezando el primer paso en 89 mm y el último en 225 mm necesitamos 5 revoluciones para cubrir los 800 mm. Se queda algo corto
Llegado a este punto el barrido lo podemos hacer por sweep de centro y radio de 44.5 mm si deseamos que sea igual en todo su recorrido.
Si deseamos que en la derecha sea más ancho que en la izquierda pues círculos de distintos tamaños en los extremos y por multisección. Ello con la hélice recta.
Si la hélice la hacemos en ángulo ( o siguiendo un perfil ) las posibilidades del resultado se multiplican.
Punto por la lección y gracias. ![]() Un saludo.
Un saludo.
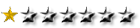
A ver, os cuento.
Lo he resuelto prácticamente, pero me da un problema porque la medida es muy justa y el inventor da error. He cambiado el tamaño de huella a 88 para que no me de el problema de que se me autointersecten los perfiles de corte, pero os voy a contar como lo he resuelto.
A partir de aquí ya es afinar por tu cuenta para obtener la solución.
Inicialmente revolucioné lo que sería la varilla inicial (eso creo que todos somos capaces de hacerlo)
Posteriormente en inventor creé la huella (en mi caso, un círculo de 88mm a 24.5 del borde, por eso de que se me intersectaba)
Después creé un boceto 3D donde definí una curva paramétrica con los siguientes valores:
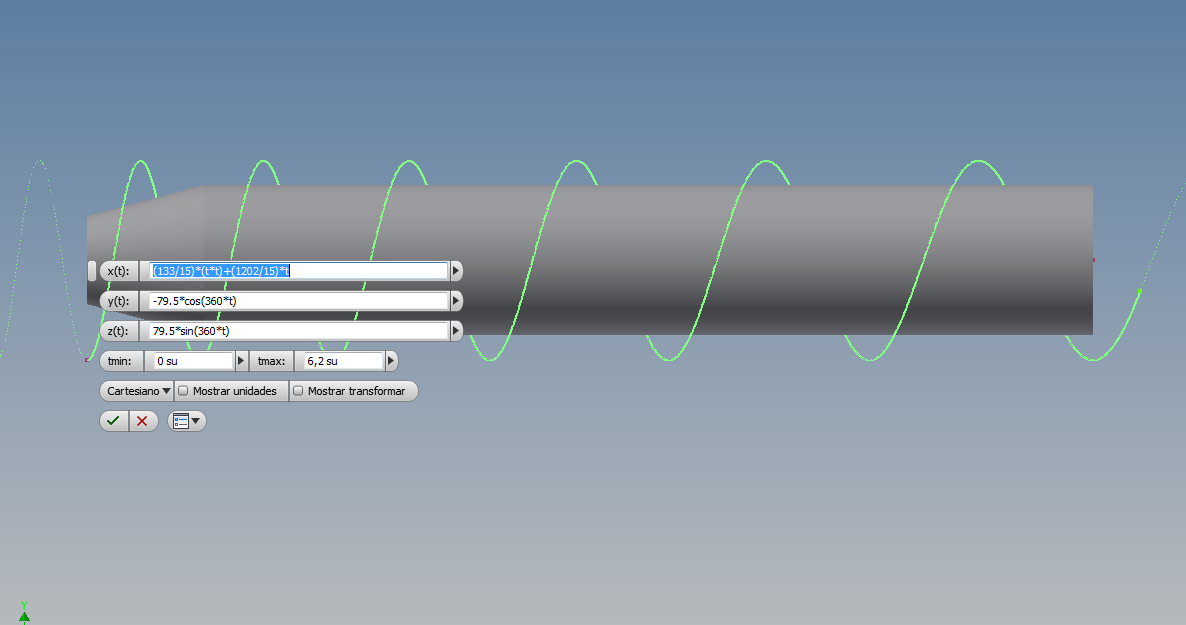
Los valores de la curva en x los hallé resolviendo el sistema de ecuaciones
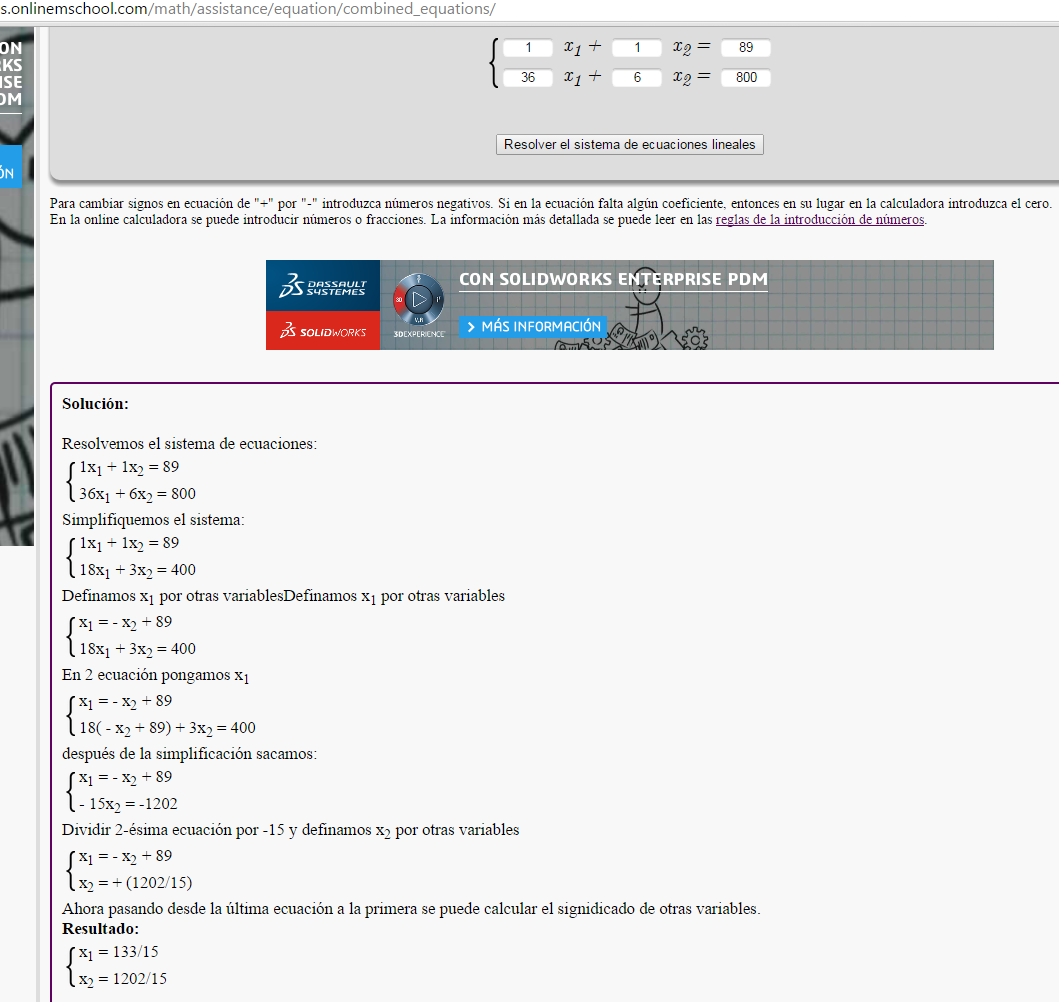
Posteriormente hice un barrido... et voilá!

edito: he cerrado ya la pieza, pero creo que con esto todos podréis hacerlo con inventor
edito 2: se me acaba de ocurrir (después de cerrar) que si en vez de hacer la huella con un círculo la hubiese hecho con un sector del mismo probablemente hubiese solucionado el problema, pero no me apetece volver a hacerlo para comprobar. Si alguno se ve con fuerzas, que pruebe
La verdad es que este sinfín de paso variable tiene su aquel. En mi caso, me he ayudado de las ecuaciones de Furlog, aunque he hecho algún cambio, he reducido el número de vueltas a 5, y ampliado los extremos para continuar el corte. La espiral la hice con Sweep.
El sistema de ecuaciones que he usado:
x1+x2=89
25x1+5x2=800
Obteniendo:
x1= 17.75
x2=71.25
Las ecuaciones de la Hélice para CATIA:
xt=79.5sin(t2PI1rad)
yt=x1(t**2)+x2t-8001mm
zt=-79.5cos(t2PI*1rad)


Furlog, he probado en Inventor y me ocurrió ese error que comentas de intersección del barrido. La solución por la que opté ha sido dividir la curva paramétrica en tres tramos: de t -0,2 a 0, de 0 a 0,9 y de 0,9 a 5,2 Así no hay problemas de intersección y se puede mantener el diámetro de 89 mm y la distancia de 25 mm.


Buenas,
Ante todo gracias por participar. Ha veis comprobado que en toda la espiral, la intersección de un cilindro perpendicular de un diámetro corra sin que penetre en el sinfin? Ese es el gran problema de este ejercicio.
En las ultimas soluciones conforme aumenta el paso el diámetro perpendicular del cilindro que intersecciona disminuye. Comprobarlo y veréis que hay que relacionar el paso con el perfil del barrido.
Saludos y reparto de puntos. ![]()
no jaam, no disminuye, puesto a que corta siempre desde la misma distancia. Si aumentas el diámetro de corte es cuando engañas al corte, al menos eso creo
puntitos para todos, de todos modos
Vamos a ver, yo sigo viendo que si dos cilindros se cortan perpendicularmente, el perfil que se genera es un circulo, no ocurre lo mismo con dos cilindros que se cortan en un ángulo cualquiera, dicho corte genera un óvalo.
El perfil que corta el sinfin(la botella), genera un óvalo variable que será tanto mayor como mayor sea el paso de la hélice.
Recordemos que la botella o el cilindro no se enrrolla, sino que se desliza siguiendo un paso manteniendo su posición vertical.
Para seguir correctamente las propuestas anteriores, la botella debería inclinarse siguiendo el paso de la hélice, cosa la cual no hace.

Bien dicho Music224.
Hola Furlong, intenta colocar unos cilindros como yo te muestro y veras que colisionan. Ya que como dice music224 tienden a ir inclinándose conforme aumenta el paso. Y la función de estos sinfines es la de separar cilindros conforme avanza.
Saludos. ![]()
Muy bien, investigando en Inventor he llegado a la conclusión que la curva que se genera a partir de que se genera una rosca; en nuestro caso el sinfin, es un óvalo.
En inventor el óvalo se puede acotar por su anchura y su altura. Podemos mantener su altura invariable y aumentar su anchura.
Esto es lo que sucede mientras la botella va avanzando a través del sinfin, a medida que aumenta el paso lo hace también la anchura de la huella.
Sin ninguna duda ello está relacionado con el ángulo de la hélice. Bien hice unos croquis geométricos y llegué a la siguiente conclusión:
El radio del óvalo en su anchura, es igual al radio de la marca que hace la botella en el cilindro, dividido por el coseno del ángulo de la hélice.
Naturalmente éste perfil va variando con el paso, ya que está en función del mismo.
Entonces podremos obtener el perfil del paso mas estrecho, y posteriormente el perfil del paso mas ancho.
Dichos perfiles quizá se puedan utilizar en Catia como el primer perfil y el segundo perfil, para generar una hélice y realizar así el corte de la misma con el perfil adecuado en un cilindro.
Dom Mar 29, 2015 17:43 - jaam_24 escribió:Bien dicho Music224.
Hola Furlong, intenta colocar unos cilindros como yo te muestro y veras que colisionan. Ya que como dice music224 tienden a ir inclinándose conforme aumenta el paso. Y la función de estos sinfines es la de separar cilindros conforme avanza.
Ahí tienes razón, yo lo había hecho con un círculo porque simplemente es lo que ponía el plano, pero es cierto que para fabricarlo se hace así
La respuesta de Music puede ser buena, sería cuestión de probar


Hola.
Después de leer todo el hilo y el que está relacionado con éste surge la siguiente duda.
¿Hay que hacer el sinfín que aparece en la lámina o se trata de diseñar un sinfín para botellas en el que no colisionen las botellas sin que sea obligatorio respetar las medidas de la lámina propuesta?
Mi opinión:
Si ese sinfín es para botellas y las botellas colisionan el problema es del diseñador, no del dibujante. El diseñador tendría que haberse preocupado de haber puesto otras cotas y/u otra geometría.
Se trata pues de modelar el sinfín con esas cotas y hacer que coincida la masa, 6.24 Kg, que aseguraría que el modelo es igual al original y por lo tanto el modelado correcto.
![]()
Saludos.