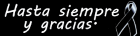OK amigos, allá va, algo breve en mi caso, pues aquí hay muchos cad diferentes, y entonces como dijimos, a por las ideas vamos.
Bueno esta sería una manera más, no muy ortodoxa, pues pretendía también practicar algunas de las maneras de mover y alinear entidades en el entorno de creación de Catia.
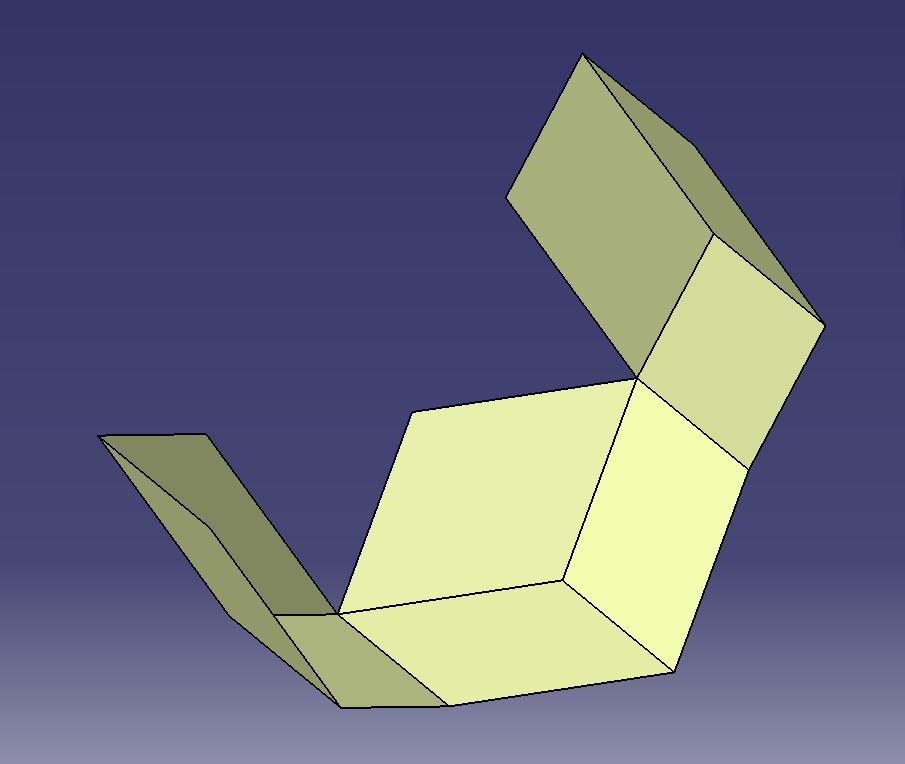
Sin pretender entrar en detalles, al parecer en todos los poliedros una manera de distinguirlos es por los tipos de vértices que tiene, y para ello se agrupan por el numero de aristas que confluyen, siendo el mínimo de tres por cada vértice, bueno..dicho sea de pasada existe una formula llamada con el nombre del descubridor “Euler†que establece que “..el numero de caras más el nº de vértices es igual que el numero de aristas mas dos,..†algo así. C+V=A+2.
Con lo que por ejemplo conociendo como es una cara del cualquier poliedro, pues podríamos sacar los números de vértices y aristas.
Y también me entretenía el tratar de ver que figuras formaban las caras, y si os fijáis en las vistas de la lamina, se aprecia un pentágono con forma de estrella en la vista superior, también hay otro mas en la inferior pero con otra orientación, “girada†para encajar con el resto de caras.
Es decir, por ahora vemos que hay vértices de 5 aristas (hemos visto de un plumazo muchas caras) . Pero es interesante saber también el mínimo de aristas que hay por vértice, y vemos que por el resto del cuerpo se aprecian figuras con vértices de 3 aristas (adicionalmente para ayudar a explicarme son esas que vistas así “parecen†cubos, por ejemplo en la vista frontal, ya que produce un efecto visual parecido a como si vieras un cubo en “isométrica†con los ejes a 120º), y lo que quería decir, estas figuras de tres rombos cada una rodean al cuerpo digamos por su parte central.
Y este es un esquema de lo que hice, para no soltaros tanto rollo, y que a veces con paciencia habéis soportado je je.
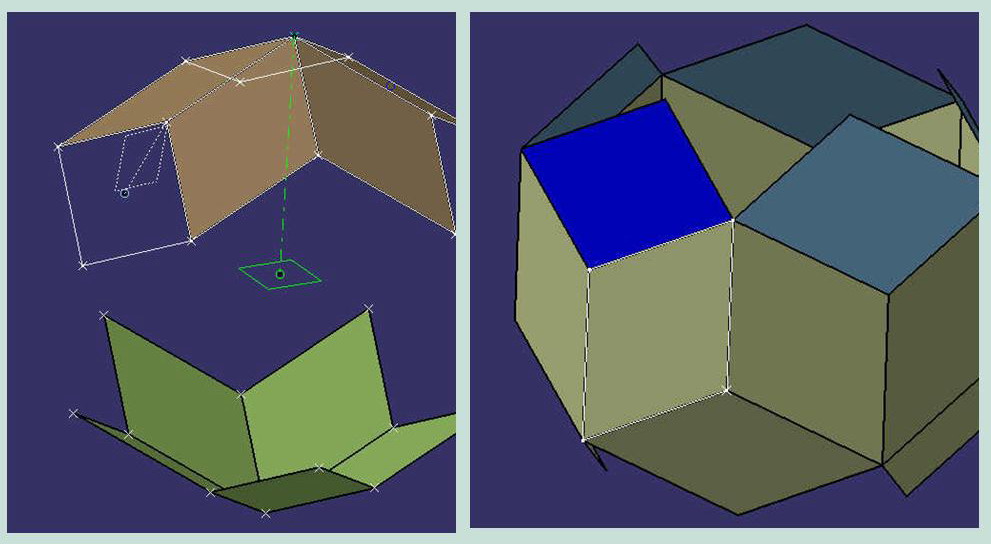
Por la parte superior se ve que completa la figura dicha con simples rombos en la postura adecuada por la parte superior, y también se ve rodeando el centro “las figuras en forma de cubosâ€
En cuanto a como forman las figuras con cada rombo, hay que destacar las disposiciones de cada uno, y si os fijáis, se intuye que en todas las figuras que imaginamos, pues usan las diagonales para alinearse, no se si me explico: En forma de estrella pentagonal unos, a 120º otros, y los simples rombos que comentaba en postura “horizontalâ€, pues es la única con que puede ya encajar con el resto.
Luego resumidamente, empecé un rombo, en el que indicaban dicha proporción entre sus diagonales, lo hice con intención de que un vértice de el fuera el de arriba, pues todavía no sabía el verdadero centro de todo el cuerpo.
En cuanto a la determinación de la dimensión de cada diagonal según esa especial proporción, me sirvió de mucho la ayuda proporcionada por nuestro amigo Juanrri, pues sugirió en su pagina como determinar esa especial proporción geométricamente, es decir con dibujo solamente. y que espero que os guste como a mi el descubrirlo, aunque quizás ya lo sabéis, permitirme facilitaros también su link . muchocatia_pista relación áurea entre dos segmentos
Siempre podríamos usar inicialmente una dimensión cualquiera en su diagonal mayor, efectuar ese trazado para sacar la otra diagonal relacionada, y por tanto formar el rombo. Y ya solo nos quedaría escalarlo para que el lado fuera 50 mm, según el ejercicio.
Entonces desde esa primera cara, forme la estrella superior usando como contaba sencillos comando de tipo traslaciones, como rotaciones y alguna simetría, para formar la figura de la estrella superior, y de paso complete los huecos de las puntas con esos otros 5 rombos “solitarios†alineando sus diagonales.
Para a continuación (dado que mi origen estaba arriba) hallar el verdadero origen del poliedro, que es donde cruzan dos normales que pasan por el medio de dos caras, y por tanto uniendo ese centro con el vértice correspondiente de mi primer rombo en la figura con forma de estrella, pues también tenía su autentico eje Z.
Estando así, si lo veis en la foto, con un plano de simetría oriente la estrella de abajo, girándola lo justo usando de referencia la misma estrella, por puntos. Observar un vértice, el punto medio en la abertura y rotarla por el eje hallado , para que así coincidiera con la otra figura de tres caras, la cual de paso también se forma fácilmente, y a la que a continuación hice una matriz polar, pues son cinco figuras también (son las que parecen un cubo)..
Es decir por figuras serian 5+5 las dos estrellas, + 5 de los rombos superiores+ 15 o (5x3) las cinco figuras centrales, o sea 30 caras.
Pero al parecer la manera de indicarlo no es esa, sino por tipos de vértices basándose primero el que menos aristas tenga, así se diría que este poliedro tiene 20 (formados por 3 aristas) + 5 (de 12 aristas)
Y voila !! que corto ¿verdad? Espero que os haya gustado, sin embargo estoy seguro que también vosotros tenéis otras maneras mas interesantes o de las que se pueda aprender, que de eso tratamos.
Un saludo y Feliz Navidad. ![]()

 -
-